How to Calculate Heat Loss

Have ever wondered how to calculate heat loss? This article, published in Process Heating, goes over the basic principles of heat transfer as well as the calculations that are used for pipes and vessels. Read more here.

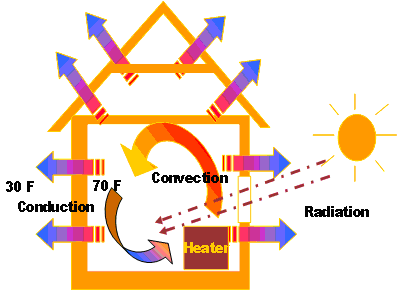
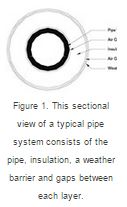
Figure 1 (below) depicts a sectional view of a typical pipe system. It consists of the pipe, insulation, a weather barrier and gaps between each layer. If the pipe and its contents are warmer than the surrounding environment, heat will be transferred from the pipe to the air. If enough heat is transferred out of the pipe, the pipe contents may thicken or solidify, resulting in damage to pipes or pumping equipment. Heat flows from one object to another in much the same way as water. Objects of unequal temperatures in a thermal system tend toward thermal equilibrium. The hotter object transfers some of its heat to the colder object until the objects are the same temperature. Heat can be transferred by way of conduction, convection and radiation.

Conduction

Conduction is defined as transferring heat or electricity through a conducting medium by way of direct contact. The rate of heat transfer is dependent upon how much resistance exists between objects of differing temperatures. In many cases, the transfer of heat from one medium to another is desired. Cooking is an everyday example of intended heat transfer. Also, most electronic components operate more efficiently if excess heat generated by the equipment is dissipated to a medium not adversely affected by the addition of heat.

Whether a substance acts as a thermal conductor or insulator depends on the thermal resistive properties of the substance. Thermal resistance (R) is a measure of an object’s ability to retard heat transfer by way of conduction through a given thickness of the substance.

Mathematically, R is: R = L/k where L is the insulation thickness in inches, and k is thermal conductivity, (BTU)(in)/(ft2)(oF)(hr)

As the thickness (L) changes, it affects the R value, or thermal resistance of an insulation. K values are constants that are specific to the physical properties of a given material. They measure a material’s ability to transfer heat. Some common K values, as measured at room temperature, of materials are 325.300 for steel, 2750.700 for copper, 0.250 for fiberglass and 0.167 for air. New Call-to-action

Convection

Losses by convection can be seen to be negligible in a system without extensive calculations. In any piping system, small air gaps exist between the surface wall and insulation. The air gaps normally are slight — less than one-tenth of an inch — and prevent the flow of air which restricts convection. Although small air gaps do not affect heat loss via convection, their thermal resistive properties should be analyzed to determine the contribution to system heat loss through conduction.
To illustrate, suppose the pipe shown in figure 1 consists of 1″ fiberglass insulation, and the air gap between the pipe wall and insulation is 0.05″. Using the R value equation, you can calculate the resistance of the insulation and air gap. A ratio of the two resistances indicates that insulation has the greatest impact in overall thermal resistance, and minor imperfections in applying insulation are minimal.

The percentage of resistance due to the air gap is 0.299 divided by 4.299, or 6.95 percent.

Radiation

Radiant heat loss occurs as a result of highly energized molecules transmitting heat by way of waves or particles. For significant heat loss to occur from radiation, the hotter surface must be well above ambient temperature — much higher than what is observed in typical heat trace applications. Therefore, heat loss from radiation can be ignored.
In practical low-to-medium temperature applications, convection and radiation account for about 10 percent of the overall heat loss of a system. By adding 10 percent, the general formula for calculating the heat loss of a system via conduction, convection and radiation can be calculated.

Flat Surface Heat Loss Calculations

The term “heat loss” commonly refers to the heat transfer of an object to its ambient environment. This implies that the object in question — a wall, for example — is at a temperature above the ambient temperature (figure 2). Mathematically, the formula for calculating the heat loss of a system through conduction, expressed in BTU/hour is:

Q = (U)(A)(T)

where U is the conductance, BTU/(ft²)(^oF)(hr)

A is the surface area of object, ft²
ΔT is the temperature difference (T1 -T2), ^oF
Conductance is the inverse of resistance, R, and can be expressed as U = 1/R or U = k/L.

Therefore, another way to express the basic heat loss (Q) is:

Q = [(k)(A)( ΔT)(1.1)] / L Heat Loss, BTU/hr

BTUS AND WATTS: A COMPARISON.

The equation above calculates the heat loss of an entire flat area in BTU/hr, but electricity is normally sold by kilowatt hours. Therefore, the equation needs a conversion factor to convert from BTU to watts. One watt equals 3.412 BTU. Modifying the equation yields a new formula:

Q = [(k)(A)( ΔT)(1.1)] / (3.412)(L) Heat Loss, W/hr

Can’t get enough information? Read more here.

To assist you in ordering the best heating system for you, please allow a knowledgeable Indeeco representative to help you today! Call 314-644-4300 or visit us at www.indeeco.com.